KONSEP NILAI WAKTU DARI UANG
Sebagai
intermezo,mungkin kita sering mendengar istilah “Time Is Money” mungkin istilah
tersebut dapat kita hubungkan dengan nilai uang terhadap waktu,dimana nilai
uang disuatu waktu tertentu akan berbeda
meskipun dengan jumlah yang sama.Kita dapat menganalogikanya dengan mudah
misalkan sewaktu orang tua saya sekolah uang 100 perak tentu begitu banyak jika
hanya untuk membeli jajanan,tetapi nilai 100 perak saat ini sudah tidak bisa
untuk membeli hal serupa pada saat dulu.
Contoh
lainya : jika seseorang diberikan pilihan untuk memilih apakah Rp. 50.000
sekarang atau uang Rp.50.000 setahun kemudian, maka tentunya ia akan memilih
uang tersebut sekarang karena jika ia memilih menerima uang tersebut sekarang,
ia akan dapat menanamkannya untuk memperoleh pendapatan bunga selama satu
tahun. Dengan demikian setahun yang akan datang, ia akan menerima Rp. 50.000
ditambah pendapatan bunga selama satu tahun atas investasinya. Jika tingkat
bunga majemuk sebesar 20% setahun, maka investasi Rp. 50.000 sekarang akan
menjadi Rp. 70.000 setahun kemudian. Jadi uang sebesar Rp. 50.000 sekarang sama
dengan nilai waktu Rp. 70.000 setahun kemudian pada tingkat suku bunga
20%.Inilah konsep nilai uang terhadap
waktu.Dapat disimpulan bahwa nilai uang disaat ini lebih besar dibadingkan
nilai uang di beberapa tahun kemudian.
Asal Mula Bunga
Asal mula bunga adalah imbal jasa atas pinjaman uang. Imbal
jasa ini merupakan suatu kompensasi kepada pemberi pinjaman atas manfaat
kedepan dari uang pinjaman tersebut apabila diinvestasikan. Jumlah pinjaman
tersbut disebut “pokok utang” (principal). Persentase dari pokok utang
yang dibayarkan sebagai imbal jasa ( bunga ) dalam suatu periode tertentu
disebut “suku bunga”
Contoh
: Raihan mengajukan kredit KPA sebesar Rp120 juta dengan jangka waktu
kredit 12 bulan, dan dikenakan bunga pinjaman sebesar 10% per tahun secara
efektif. Berapakah angsuran per bulan yang harus dibayar?
Data:Pokok pinjaman: Rp120.000.000
Bunga per tahun: 10%
Tenor pinjaman: 12 bulan
Cicilan pokok:
Rp120.000.000 : 12 bulan = Rp10.000.000/bulan
Bunga bulan 1:
((Rp120.000.000 - ((1-1) x Rp10.000.000)) x 10% : 12 = Rp 1.000.000
Maka, cicilan bulan 1 = Rp10.000.000 + Rp1.000.000 = Rp11.000.000 dst.
Bunga Sederhana
Apabila bunga total yang dikenakan berbanding linier dengan
besarnya pinjaman awal, tingkat suku bunga dan periode waktu,maka
tingkat bunga tersebut dikatakan sederhana. Bunga sederhana jarang
digunakan dalam praktek komersial modern.
Total bunga (I) yang diperoleh atau dibayar dapat dihitung
dengan rumus sebagai berikut:
I = (P) (N) (i) (3.1)
Dengan :
P = jumlah uang pokok yang dipinjamkan atau dipinjam
N = jumlah periode bunga (misalnya : tahun)
I = tingkat suku bunga tiap periode bunga
Jumlah total yang harus dibayar pada akhir N periode bunga
adalah P + I
Contoh :
Rp. 5.000 dipinjamkan selama tiga tahun pada tingkat suku bunga
15% tiap tahun. • Bunga yang diperoleh adalah : I = Rp. 5.000 x 3x 0,15 = Rp. 2250 • Sedangkan total perolehan pada akhir tiga tahun adalah Rp.
5.000 + Rp. 2.250 = Rp. 7.250
Perlu diperhatikan bahwa jumlah kumulatif dari bunga yang
diperoleh adalah fungsi linier dari waktu hingga bunga dibayar.
Bunga Majemuk
Apabila bunga yang dibebankan untuk setiap periode (satu
tahun, misalnya) didasarkan pada sisa pinjaman pokok ditambah setiap
beban bunga yang terakumulasi sampai dengan awal periode itu,
29
bunga itu disebut bunga majemuk atau bunga berbunga (compound
interest). Pengaruh bunga majemuk dapat terlihat, yaitu untuk pinjaman sebesar Rp. 5.000 selama dua tahun pada
tingkat bunga sebesar 15% per tahun.
No.
|
(1) Jumlah Pinjaman pada Awal Periode
|
(2) = (1) x 10% Jumlah bunga untuk
Periode
|
(3) = (1) + (2) jumlah Pinjaman pada
Akhir Periode
|
1.
|
Rp.5.0000
|
2250
|
7520
|
2.
|
7520
|
2475
|
9995
|
3.
|
9995
|
Rp.247.5
|
Rp.10.242,5
|
bunga sederhana. Untuk pembahasan selanjutnya, apabila tidak ada
keterangannya berarti bunga yang digunakan adalah bunga majemuk.
Keekivalenan
nilai uang yang berbeda pada waktu yang berbeda akan tetapi secara finansial mempunyai nilai yang sama.Kesamaan nilai finansial tersebut dapat ditunjukkan jika nilai uagng dikonversikan (dihitung) pada satu waktu yang sama
Keekivalenan = Jumlah pinjaman/Jangka waktu pinjaman
Notasi dan Diagram/tabel Arus Kas
NOTASI, DIAGRAM DAN TABEL ARUS KAS
Notasi berikut ini digunakan dalam rumus-rumus hitungan
bunga bersusun
i = tingkat suku bunga efektif tiap periode bunga.
N = jumlah periode penyusunan.
P = jumlah uang pada saat ini; nilai ekivalen dari satu atau
lebih arus kas pada suatu waktu tertentu yang disebut
saat ini (present).
F = jumlah uang pada saat ini; nilai ekivalen dari satu
atau lebih arus kas pada suatu waktu tertentu yang
disebut waktu yang akan datang (future).
A = arus kas pada akhir periode (nilai ekivalen pada
akhir periode) dalam bentuk seragam yang berseri
berkelanjutan selama sejumlah periode tertentu, dimulai
dari akhir periode pertama dan berkelanjutan sampai
periode terakhir.
Pemakaian diagram kas (waktu) dan/atau tabel sangat
direkomendasikan untuk keadaan dimana analis memerlukan penjelasan
atau visualisasi apa yang terlibat ketika aliran uang terjadi selama
40
waktu yang berbeda. Selisih antara total arus masuk (penerimaan)
dan total arus keluar (pengeluaran) selama periode waktu
tertentu (misalnya: satu tahun) adalah arus kas bersih selama satu
periode. Arus kas penting dalam ekonomi teknik karena merupakan
dasar dari evaluasi alternatif. Fungsi diagram arus kas dalam ekonomi
teknik adalah analog dengan free body diagram dalam problem
mekanika.
Gambar 3.2. dan gambar 3.3 menunjukkan diagram arus kas (cash
flow). Dua gambar ini juga menggambarkan definisi dari simbol-simbol
yang telah diuraikan di atas dan penempatannya pada diagram arus
kas. Perhatikan bahwa semua arus kas telah ditempatkan pada akhir
tahun agar cocok dengan perjanjian yang digunakan.
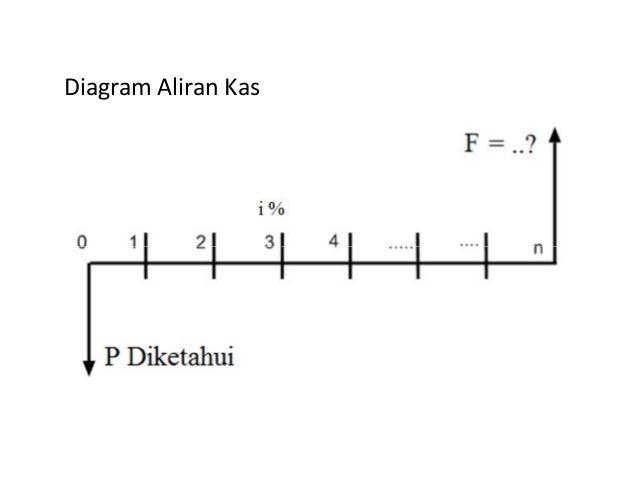
Diagram arus kas menggunakan beberapa ketentuan: 1. Garis horisontal adalah skala waktu, dengan pertambahan waktu
bergerak dari kiri ke kanan. label periode (misalnya: tahun,
seperempat tahun, bulan) dapat ditempatkan pada interval
waktu selain titik waktu dalam skala waktu. Misalnya akhir dari
periode 2 adalah sama dengan awal periode 3. ketika perjanjian arus
kas akhir periode digunakan, nomor periode dapat ditempatkan pada
akhir tiap interval waktu seperti ditunjukkan pada gambar di atas.
42
2. Anak panah menunjukkan arus kas kas dan ditempatkan di akhir
periode. arah ke bawah mewakili pengeluaran (arus kas negatif atau
arus kas keluar), sedangkan arah ke atas mewakili pemasukan
(arus kas positif atau arus kas masuk).
3. Diagram arus kas tergantung pada sudut pandangnya.
Misalnya, situasi yang ditunjukkan pada gambar-gambar di atas
berdasarkan pada arus kas dari sudut pandang yang memberi
pinjaman. Jika arah semua anak panah dibalik, persoalan
digambarkan dari sudut pandang peminjam.
Tidak Diketahui Nilai Awal,Diketahui nilai akan datang
Pada akhir n periode,
jumlah ini akan tumbuh menjadi : F=(I+I)^N
Contoh : Jika kamu meminjam uang sebesar Rp
8.000 sekarang,
perjanjianya pengembalian pinjaman pokok
ditambah akumulasi bunga
selama 4 tahun pada i=10% tiap tahun. Berapa
yang harus dibayarkan
pada akhir tahun?
Gradien seragam
Pada
deret gradien panjangnya periode adalah N, tetapi aliran kas dalam periode 1
adalah 0. Beberapa faktor yang mempengaruhi gradien antara lain nilai sekarang,
annuitas, atau nilai masa akan datang.
P
= G (P/G, i, N) atau G = P (G/P, i, N) (3.9)
A
= G (A/G, i, N) atau G = A (G/A, i, N) (3.10)
F
= G (F/G, i, N) atau G = F (G/F, i, N) (3.11)
Beberapa
masalah arus kas melibatkan peneriman-peneriman atau pengeluaran-pengeluaran
yang diproyeksikan agar meningkat atau berkurang.
Jumlah
secara konstan, G, pada setiap periode. Situasi itu dapat dimodelkan dengan
suatu kemiringan/gradient yang seragam (uniformgradient/arithmetic gradient).
BUNGA NOMINAL
Tingkat
suku bunga biasanya ditetapkan secara tahunan. Penggunaan
perjanjian-perjanjian yang dibuat memungkinkan tingkat suku bunga untuk
diatur secara khusus sehingga bunga dapat dibayarkan beberapa kali dalam satu
tahun. Misalnya, per bulan, per tiga bulan, per enam bulan, & sebagainya.
Sebagai
contoh, pembayaran selama satu tahun dapat dibagi menjadi empat kali tiga
bulanan dengan tingkat suku bunga 3% per tiga bulan. Sama halnya jika
dikatakan 12% dibayarkan per tiga bulan dalam satu tahunnya. Biasanya,
tingkat suku bunga itu dikatakan sebagai “12% yang bersusun setiap 3 bulan”.
Apabila dinyatakan dengan cara tersebut, maka tingkat suku bunga 12% disebut
tingkat suku bunga nominal dan dinyatakan dengan notasi r.
Nilai
mendatang untuk pinjaman sebesar Rp 10.000,- pada akhir tahun pertama dengan
tingkat suku bunga 12% yang bersusun setiap tiga bulan adalah:
F4 =
10.000(1+0.03)4 = 11.255,0881
Apabila
disepakati untuk menggunakan tingkat suku bunga 12% yang dibayarkan hanya
sekali di akhir tahun, maka:
F1 =
10.000(1+0.12)1 = 11.200
Pembayaran
bunga yang dilakukan lebih dari sekali dalam satu tahun mengakibatkan nilai
di akhir tahun lebih besar dibandingkan dengan jika bunga hanya dibayarkan
sekali dalam satu tahun
·
BUNGA EFEKTIF
Jika
pembayaran bunga dilakukan lebih dari sekali dalam setahun, tingkat suku
bunga sesungguhnya akan lebih tinggi daripada tingkat suku bunga nominal.
Tingkat suku bunga sesusungguhnya atau yang dibayarkan secara tepat pada
pinjaman selama setahun disebut tingkat suku bunga efektif.
Tingkat
suku bunga efektif biasanya dinyatakan per tahun, kecuali bila dinyatakan
lain secara khusus. Tingkat suku bunga efektif dinyatakan dengan notasi i.
Hubungan antara tingkat suku bunga efektif,i, dan tingkat suku bunga
nominal,r, adalah:
Contoh :
Apabila
suku bunga nominal per tahun adalah 20%, yang mana dalam satu tahun terdiri
dari 4 kuartal, Berapakah besarnya suku bunga nominal untuk setiap bunga
kuartal
· r = 20%
· M =4
· i = r /
M = 20% / 4 = 5% per kuartal
Berapa
pula suku bunga efektif per tahunnya?
Ieff = (1 + i)M -1
= (1 +
0,05)4 - 1
= 0,2155
atau 21,55% per tahun
Sumber Referensi : http://dsuryap.blog.com/2011/05/21/bunga-nominal-dan-bunga-efektif/ |





Tidak ada komentar:
Posting Komentar